GEOMETRIA: Preparando el final Blumenfarb: Matemática 2. Finales resueltos.

Bueno, vamos a tratar de hacer las preguntas de los finales y posiblemente resolverlas.
Esto es lo que yo pienso que tengo q responder. Si tenes alguna aclaración o pensas que algo está mal te invito a que me lo digas y te lo agradezco!
Este final es ampliamente teórico. La teoría de la matematica de los temas que dieron sobre el año. Si prestas mucha atención en clase y tomaste nota de hasta la cosa más insignificante en ese momento (como la aplicación de las cosas al diseño) fuiste inteligente. Yo no, y estoy aprendiendo como puedo.

Vamos a empezar con el punto uno, que siempre es de geometría:

Pregunta de un final 2012:
-Definir superficie reglada, dar ejemplos númericos y mencionar aplicación al diseño.

Se llama superficies regladas a las engendradas por rectas paralelas a una dirección dada variable, que se desplazan por una curva llamada directriz. Hay distintos tipos de superficies regladas. Las superfices cílindricas son generadas por rectas paralelas a si misma apoyadas en una curva, directriz, las rectas que generan las superfices se llaman generatrices.
Es una superficie cilindrica si las generatrices son perpendiculares al plano que contiene la directriz.
Una ecuación que contenga dos variables si representa una curva en el plano de dichas variables, será la ecuación de una superficie cílindrica recta, cuyas generatrices son paralelas al eje de la variable faltante o ausente.
Además estan las superficies cónicas, las cuales son generadas cuando la generatriz se desplaza por la curva directriz pero atraviesa un vertice no perteneciente al plano de la curva.

Pregunta de un final 2009, 2010:
-Hipérbola, con sus definiciones (integración con el plano, sistema de puntos) Ejemplo gráficado, ecuación, usos en arquitectura.
La hipérbola es el lugar geométrico de los puntos en donde la diferencia de sus distancias a dos puntos fijos, los focos, es siempre constante. Si se corta con un plano a una superficie cónica en ángulo paralelo al eje se obtiene una hipérbola.
Gráficos y propiedades y ecuación en este video explican muy bien:

Pregunta de un final 2009, 2010, 2012:

-Definir superficies cónicas, cuándo se obtiene un cono circular recto, y curvas que salen de este. 

Una superficie cónica es una superficie reglada, puede ser de revolución o de no revolución. Se trata de una recta, la generatriz, la cuál se apoya en una curva, la directriz, y pasa por un punto, el vertice el cual está no está en el mismo plano que la directriz.

Una superficie cónica de revolución es engendrada cuando la generatriz rota alrededor de una recta fija, el eje. La generatriz corta al eje en un punto, el vertice.

Es un cono circular recto si la directriz es una circunferencia.

Las curvas que salen de un cono circular recto son: Al cortar el cono en un ángulo paralelo al eje se obtiene una hipérbola, en un ángulo paralelo a la generatriz, una parabola. Si corta en ángulo diferente a la generatriz se da un elipse, y si se corta en el plano con ángulo igual a 0° se da una circunferencia

Ecuación del cono:

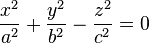
Pregunta final 2009, 2010, 2011, 2012, 2013:

-Definir la elipse como conjunto de puntos y interseccion entre superficies. ¿Cuál es su ecuación en un sistema cartesiano de ejes? ¿Cuáles son las dos relaciones que existen entre sus parámetros? ¿a que se le llama excentricidad y que relacion mide? Dar un ejemplo numerico de lo expuesto anteriormente. Mencionar alguna aplicación de la misma al diseño.

La elipse es el lugar geométrico de todos los puntos de un plano tales que la suma de las distancias a otros dos puntos fijos, los focos, es constante. La elipse se da cuando se intersecta con un plano en ángulo distinta a la generatriz en una superficie cónica de revolución.

Ecuación cartesiana

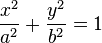
Entre a, b y c existe la relación pitagórica ya que se puede armar un triángulo rectángulo entre ellas.

a es el semi eje mayor, b es el semi eje menor y c la distancia entre el centro y el foco.

La excentricidad caracteriza la forma del elipse. 

Se define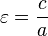 

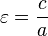
Cuanto más próximo a cero sea el valor de la excentricidad más redondeada es la elipse.

Pregunta final 2009, 2010:

1) A q se llama superficie cilíndrica? Graficar al menos 2 ejemplos de las mismas y dar sus respectivas ecuaciones referidas a un sistema cartesiano de ejes.
Mencionar algunas aplicaciones concretas de ellas al diseño-

Una superficie cilíndrica es generada por una recta que se desplaza paralelamente a si misma apoyada en una curva directriz. Una ecuación que contenga dos variables, si representa una curva en el plano de dichas variables, será la ecuación de una superficie cilíndrica recta cuyas generatrices son paralelas a la variable faltante.

EJ:

Cilíndro eliptico 

 

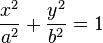
Cilíndro parabólico

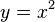
Pregunta final 2009, 2010, 2012:

Esta es bastante dificil de entender.... yo escribo lo que puedo, pero el ejemplo, como sacar focos, directriz etc es complicado ahi va:

Explique cómo se obtiene a partir del concepto de conjunto de puntos en el plano la ecuación de la parábola con vértice en el origen. Mostrar un ejemplo numérico de parábola desplazada y graficarla indicando su vértice, foco y directriz 

Se denomina parábola al lugar geométrico de los puntos de un plano que equidistan de una recta dada, la directriz, y de un punto exterior a ella, el foco.

Les dejo un video que explica como sacar los vertices y focos de una parabola desplazada. El tema es que la ecuación para sacar estos datos estan al cuadrado y hay que saber traducir una ecuación normal completando cuadrados para dejarla de la forma que te deja sacar los datos.

Pregunta final 2010:

-Que es una superficie de revolucion? Definirla. Dar las ecuaciones de 2 de ellas y graficarlas mostrando su orientacion en el espacio y sus intersecciones con los ejes coordinados. Indicar si las mismas pueden ser regladas. Justificar.

Se dice que una superfice es de revolución si está engendrada por la rotación de una curva, la generatriz, alrededor de una recta fija, el eje, contenida en el plano de la curva.

Ejemplo uno: Cono Circular recto:

Ecuación

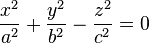
Puede ser una superficie reglada, como directriz se utilizaría una circunferencia y las reglas deberian pasar por un vertice. El cono es una cuádrica degenerada.

Ejemplo dos: Paraboloide elíptico

Si además es a = b, el paraboloide elíptico será un paraboloide de revolución, que es la superficie resultante de girar una parábola en torno a su eje de simetría. Las antenas parabólicas son paraboloides de revolución, y tienen la propiedad de reflejar los rayos paralelos entrantes hacia su foco, punto donde se ubica el receptor.

Esto último lo copie de wikipedia.

No puede ser superficie reglada ya que no podria proyectarse un paraboloide eliptico a traves de una directriz y generatriz.

------------------------------------------------------------------------------------------------------------

EN FIN.... estas son todas las que hice de geometría por ahora, que no es poco. Próximamente grafos. Hay que estudiar mucho, porque creo que hay más preguntas y son todas amplias...

Suerte, yo estoy tratando de rendir ahora en marzo 2014.