Bueno, curse A2 en Carnicer. Y aca mando algunas imagenes
martes, 2 de diciembre de 2014
miércoles, 26 de noviembre de 2014
martes, 2 de septiembre de 2014
jueves, 28 de agosto de 2014
Entrega mitá de año Carnicer A2
Y ya que estamos vamos con los renders de la entrega de mitad de año. Era un centro de salud en langostura.
domingo, 30 de marzo de 2014
Resumen 2013. El lunes arranca el 2014
Ahora el lunes 31 de marzo arranca devuelta la facultad.
Inscripto en tres materias por ahora,
A2 en Carnicer
I2 en Roscardi
E1 en Roizen creo el sabado a la mañana, después vendran los comentarios..
En el 2013
Hice A1 en Moscato, que estuvo bueno. Aprendí mucho la verdad, pero ahora me quiero cambiar. No quiero seguir con Moscato un año más, me gustó más lo que vi en Carnicer así que voy a probar.
Igual para primer año me pareció muy buena.
Instalaciones 1, en Roscardi. Ya dí la opinión, lo mismo con RA.
Morfología 1, en Doberti la deje.... no me gustó. No me gustó la forma en q se trabajaba, menos como me corregían jaja... no me gusta la materia. Habia hecho SRG en Lombardi mil veces mejor. Morfología ahi me dijeron que es muy dificil.
Construcciones en Gomez Diz.... No comment. Me falta el final todavia. Me voy a anotar para hacer C2, pero porque soy mediocre a veces y laburando y yendo a la facultad si puedo hacer una materia liviana mejor.
Inscripto en tres materias por ahora,
A2 en Carnicer
I2 en Roscardi
E1 en Roizen creo el sabado a la mañana, después vendran los comentarios..
En el 2013
Hice A1 en Moscato, que estuvo bueno. Aprendí mucho la verdad, pero ahora me quiero cambiar. No quiero seguir con Moscato un año más, me gustó más lo que vi en Carnicer así que voy a probar.
Igual para primer año me pareció muy buena.
Instalaciones 1, en Roscardi. Ya dí la opinión, lo mismo con RA.
Morfología 1, en Doberti la deje.... no me gustó. No me gustó la forma en q se trabajaba, menos como me corregían jaja... no me gusta la materia. Habia hecho SRG en Lombardi mil veces mejor. Morfología ahi me dijeron que es muy dificil.
Construcciones en Gomez Diz.... No comment. Me falta el final todavia. Me voy a anotar para hacer C2, pero porque soy mediocre a veces y laburando y yendo a la facultad si puedo hacer una materia liviana mejor.
miércoles, 12 de marzo de 2014
Matematica II Blumenfarb: Aprobado! - Final Marzo 2014
Bueno, aprobé finalmente, y les traigo lo que me tomaron. Me saqué un 7. Contesté todo. No se en que me equivoque... un poco de cada cosa seguramente. El final son 100 puntos, y calculo que saqué 70 de 100.
Escuché que apartir del curso de verano 2014 van a agregar cosas a los próximos finales. Para los que no lo hicieron, o reprobaron tengan en cuenta. No se que es lo que van a agregar. Hay q averiguar.
Ahí va el final:
1) Geometría (25 puntos): Definir superficie cílindrica. Dar dos ejemplos númericos, graficarlo junto a sus trazas. citar alguna aplicación concreta del diseño de cada una de las superficies mencionadas.
Esto está explicado aca en el blog... las trazas solo dibuje la directriz y la aplicación al diseño chamuye lo primero que se me vino a la mente.
2) Grafos y Simetría(15 puntos) : Definir mosaico. ¿Qué polígonos son los que permiten el recubrimiento del plano? Justificar matemáticamente la razon de porque solamente ellos lo permiten. Enunciar el problema de coloración y mediante substracción y adición de areas crear un mosaico indicando los movimientos realizados para lograrlo.
También respuestas podes encontrar aca.
3)Integrales y derivadas (25 puntos) : ¿Qué aplicaciones físicas de la integral conoce? Mencionar dos y dar sus formulas de cálculos. Dar ejemplos númericos para los dos y resolver.
Yo acá pensé que me habia equivocado pero no, debe estar bien. Puse area bajo la curva, que es el integral normal. Y volumen de revolución con su formula.
4) Variable aleatoria (20 puntos) Definir. Cuando es discreta y cuando es continua. Dar un ejemplo de cada una y resolver uno...
esta es la más dificil ya q no habia estudiado bien estadistica. Resolvi el ejemplo de discreta.
5) Topografía (15 puntos): Enunciar teorema del coseno y proponer un ejemplo númerico donde el uso del mismo es imprescindible.
No lo había estudiado. Me vino una luz del cielo y me acordé.
Sólo puse la formula y explique cuando era necesario.
Escuché que apartir del curso de verano 2014 van a agregar cosas a los próximos finales. Para los que no lo hicieron, o reprobaron tengan en cuenta. No se que es lo que van a agregar. Hay q averiguar.
Ahí va el final:
1) Geometría (25 puntos): Definir superficie cílindrica. Dar dos ejemplos númericos, graficarlo junto a sus trazas. citar alguna aplicación concreta del diseño de cada una de las superficies mencionadas.
Esto está explicado aca en el blog... las trazas solo dibuje la directriz y la aplicación al diseño chamuye lo primero que se me vino a la mente.
2) Grafos y Simetría(15 puntos) : Definir mosaico. ¿Qué polígonos son los que permiten el recubrimiento del plano? Justificar matemáticamente la razon de porque solamente ellos lo permiten. Enunciar el problema de coloración y mediante substracción y adición de areas crear un mosaico indicando los movimientos realizados para lograrlo.
También respuestas podes encontrar aca.
3)Integrales y derivadas (25 puntos) : ¿Qué aplicaciones físicas de la integral conoce? Mencionar dos y dar sus formulas de cálculos. Dar ejemplos númericos para los dos y resolver.
Yo acá pensé que me habia equivocado pero no, debe estar bien. Puse area bajo la curva, que es el integral normal. Y volumen de revolución con su formula.
4) Variable aleatoria (20 puntos) Definir. Cuando es discreta y cuando es continua. Dar un ejemplo de cada una y resolver uno...
esta es la más dificil ya q no habia estudiado bien estadistica. Resolvi el ejemplo de discreta.
5) Topografía (15 puntos): Enunciar teorema del coseno y proponer un ejemplo númerico donde el uso del mismo es imprescindible.
No lo había estudiado. Me vino una luz del cielo y me acordé.
Sólo puse la formula y explique cuando era necesario.
jueves, 6 de marzo de 2014
Final de Matemática 2 - Cátedra Blumenfarb - Diciembre del 2012 - Otro más.
Acá tratando de resolver otro.....
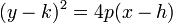
2-grafo poligonales, cuando es regular y completamente regular, cuales poliedros son regulares y graficar tres de ellos
3-Interpretación geometrica de la derivada y física, dar ejemplo de cada una
Ejemplo: Si A es sacar una Bola negra y B sacar una roja, si se saca una bola de la bolsa no puede ser roja y negra a la vez. Son sucesos excluyentes.. Si C es sacar una bola cualquiera A interseccion C y B interseccion C existen por ende son NO excluyentes o compatibles. Ahora si saco una bola y la vuelvo a meter en la bolsa la probabilidad de sacar una roja o una negra es siempre la misma por ende son sucesos independientes.

Final de Matemática 2 - Cátedra Blumenfarb - Diciembre del 2012 - Arquitectura
Materia: Matemática 2
Cátedra: Blumenfarb
Universidad: FADU - UBA - Argentina
Fecha aproximada del examen: Diciembre del 2012
El examen fue: Escrito
Alumno/a: troupa
Lo que tomaron:
1-parábola, definición como conjunto de puntos y intersección de planos, ecuación de parábola de eje horizontal
Cátedra: Blumenfarb
Universidad: FADU - UBA - Argentina
Fecha aproximada del examen: Diciembre del 2012
El examen fue: Escrito
Alumno/a: troupa
Lo que tomaron:
1-parábola, definición como conjunto de puntos y intersección de planos, ecuación de parábola de eje horizontal
Se denomina parábola al lugar geométrico de los puntos de un plano que equidistan de una recta dada, la directriz, y de un punto exterior a ella, el foco.
La paraábola se obtiene como intersección de planos al cortar una superficie cónica en ángulo igual al de la generatriz.
Ecuación de una parabola con eje horizontal, eje en Y
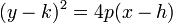
2-grafo poligonales, cuando es regular y completamente regular, cuales poliedros son regulares y graficar tres de ellos
Grafo Poligonal: Un graafo plano conexo que es runion de ciclos tal que existe un ciclo mínimo y otro máximo. Un grafo poligonal divide el plano en zonas polígonales. El interior de cada ciclo se llama cara. En un grafo poligonal puede comprobarse que el numero de caras + vertices = aristas más dos.
Un grafo poligonal es regular cuándo el grado de cada vertice es el mismo.
Es completamente regular cuándo cada cara límita con la misma cantidad de aristas.
Los poliedros regulares son el tetraedro, el hexaedro, octahedro, icosaedro, dodecaedro.
3-Interpretación geometrica de la derivada y física, dar ejemplo de cada una
El video que puse antes para explicar la aplicacion geometrica de la derivada, esta en el posts que se llama Derivadas...
Y la fisica esta bien explicada en este link
http://www.dervor.com/derivadas/interpretacion_derivada.html
4-cuando la probabilad es excluyente y no excluyente, definir probabilidad independiente, dar ejemplos de cada uno con 2 bolas de color negro y 3 rojas
La probabilidad es excluyente o incompatible cuando dos sucesos no puede suceder a la vez.
La probabilidad es no excl cuando dos sucesos pueden ocurrir a la vez.
Sucesos independientes son cuando la probabilidad de que ocurra un suceso determinado, por ejemplo A, sea la misma habiendo ocurrido o no el suceso B.
Ejemplo: Si A es sacar una Bola negra y B sacar una roja, si se saca una bola de la bolsa no puede ser roja y negra a la vez. Son sucesos excluyentes.. Si C es sacar una bola cualquiera A interseccion C y B interseccion C existen por ende son NO excluyentes o compatibles. Ahora si saco una bola y la vuelvo a meter en la bolsa la probabilidad de sacar una roja o una negra es siempre la misma por ende son sucesos independientes.
5-como se halla el area de un terreno con forma de cuadrilátero, con dos ángulos congruentes (mismo angulo) y adyacentes (continuo)
Creo que se divide con la diagonal el cuadrilatero en dos triangulos y obteniendo más datos, la distancia de diagonal y dos angulos internos por cada triangulo puede obtenerse los datos de todos los lados y luego sacar el area de los triangulos usando la relacion del seno con el area en la formula:

---------------------------------------------------------------
Mañana rindo lrpmqlp.
Con un 4 estoy más feliz que ganar 5 lucas en una raspadita. Va no se, tampoco para tanto.
miércoles, 5 de marzo de 2014
Final de Matemática 2 - Cátedra Blumenfarb - Julio del 2012 - Arquitectura - Resuelto por mi
Materia: Matemática 2
Cátedra: Blumenfarb
Universidad: FADU - UBA - Argentina
Fecha aproximada del examen: Julio del 2012
El examen fue: Escrito
Alumno/a: tomson
Lo que tomaron:
GEOMETRIA --> Definir superficies regladas, cuales son y dar dos ejemplos numericos y graficar. Ejs de arquitectura de ellos
Se llama superficies regladas a las engendradas por rectas, generatrices, paralelas a una dirección dada variable, que se desplazan por una curva llamada directriz. Hay dos tipos de superficies regladas, las cílindricas y las cónicas. En las superficies cílindricas las generatrices son paralelas entre sí, y en las cónicas las generatrices se apoyan en la directriz y pasan todas por un punto fijo, el vertice.
Si las generatrices son perpendiculares al plano de la directriz, son superficies cílindricas rectas. Una ecuación que contenga dos variables, si representa a una curva en el plano de dichas variables, esta será la ecuación para una superficie cílindrica recta cuyas generatrices son paralelas al eje de la variable faltante o ausente.
Ej: Cílindrico elíptico y cílindro hiperbólico
GRAFOS --> Cuando un grafo es regular y completamente regular. Que poliedros son completamente regulares. Que dice la formula de Euler, y cual es la condicion para que los grafos cumplan dicha formula
Un grafo regular es un grafoen donde el grado de todos los vertices son el mismo.
Un grafo es completamente regular si todas las caras limitan con la misma cantidad de aristas.
Los poliedros regulares son el tetraedro, el hexaedro, el ocatedro, el dodecaedro y el icosaedro.
La formula de euler dice que las caras + vertices = aristas + dos.
Para que se cumpla dicha condición el grafo debe ser plano y conexo.
DERIVADAS E INTEGRALES --> Integral definida cuales son sus aplicaciones geometricas, dar un ejemplo sencillo de cada una y resolver
Las aplicaciones de la integral definida son el cálculo de volumen, el cálculo del area y la longitud de curva.
Y bueno despues agarré la funcion e hice ejemplo numerico para cada situación usando las formulas q estan el post de integrales.
PROBABILIDAD Y ESTADISTICA --> Definir variables aleatorias y cuales son los dos tipos (continuas y discretas). Teniendo una bolsa con bollias de dos colores armar un ejercicio y resolverlo teniendo en cuenta las variables aleatorias discretas,
Esta es complicada... estadistica es más compleja que probabilidad.
Si se tiene una variable real cuyo dominio es un espacio muestral de E y a cada uno de sus valores, o intervalo de valores, se le asigna una probabilidad, entonces es una variable aleatoria.
El numero de veces que la variable toma un determinado valor es estimado. En los experimentos en los cuales la variable aleatoria se cuenta es discreta y en los cuales se mide es continua.
Ej: Se tiene una bolsa de bolillas con igual cantidad de bolillas de cada color. Solo hay rojo y amarillo. E sería el espacio muestral del experimento aleatorio que consiste en sacar 3 bolillas de la bolsa, y X sería la función de E al cual cada elemento se le asigna la cantidad de bolillas rojas sacadas. X es una variable aleatoria que toma los valores:
x = 0
x = 1
x = 2
x = 3
Quedaría:
f(0) = P (x=0) = 1/8
f(1) = P (x=1) = 3/8
f(2) = P (x=2) = 3/8
f(3) = P (x=3) = 1/8
TOPOGRAFIA --> Cuadrilatero con un solo angulo recto, poner los datos minimos necesarios para resolver, y luego resolver.


Cátedra: Blumenfarb
Universidad: FADU - UBA - Argentina
Fecha aproximada del examen: Julio del 2012
El examen fue: Escrito
Alumno/a: tomson
Lo que tomaron:
GEOMETRIA --> Definir superficies regladas, cuales son y dar dos ejemplos numericos y graficar. Ejs de arquitectura de ellos
Se llama superficies regladas a las engendradas por rectas, generatrices, paralelas a una dirección dada variable, que se desplazan por una curva llamada directriz. Hay dos tipos de superficies regladas, las cílindricas y las cónicas. En las superficies cílindricas las generatrices son paralelas entre sí, y en las cónicas las generatrices se apoyan en la directriz y pasan todas por un punto fijo, el vertice.
Si las generatrices son perpendiculares al plano de la directriz, son superficies cílindricas rectas. Una ecuación que contenga dos variables, si representa a una curva en el plano de dichas variables, esta será la ecuación para una superficie cílindrica recta cuyas generatrices son paralelas al eje de la variable faltante o ausente.
Ej: Cílindrico elíptico y cílindro hiperbólico
GRAFOS --> Cuando un grafo es regular y completamente regular. Que poliedros son completamente regulares. Que dice la formula de Euler, y cual es la condicion para que los grafos cumplan dicha formula
Un grafo regular es un grafoen donde el grado de todos los vertices son el mismo.
Un grafo es completamente regular si todas las caras limitan con la misma cantidad de aristas.
Los poliedros regulares son el tetraedro, el hexaedro, el ocatedro, el dodecaedro y el icosaedro.
La formula de euler dice que las caras + vertices = aristas + dos.
Para que se cumpla dicha condición el grafo debe ser plano y conexo.
DERIVADAS E INTEGRALES --> Integral definida cuales son sus aplicaciones geometricas, dar un ejemplo sencillo de cada una y resolver
Las aplicaciones de la integral definida son el cálculo de volumen, el cálculo del area y la longitud de curva.
Y bueno despues agarré la funcion e hice ejemplo numerico para cada situación usando las formulas q estan el post de integrales.
PROBABILIDAD Y ESTADISTICA --> Definir variables aleatorias y cuales son los dos tipos (continuas y discretas). Teniendo una bolsa con bollias de dos colores armar un ejercicio y resolverlo teniendo en cuenta las variables aleatorias discretas,
Esta es complicada... estadistica es más compleja que probabilidad.
Si se tiene una variable real cuyo dominio es un espacio muestral de E y a cada uno de sus valores, o intervalo de valores, se le asigna una probabilidad, entonces es una variable aleatoria.
El numero de veces que la variable toma un determinado valor es estimado. En los experimentos en los cuales la variable aleatoria se cuenta es discreta y en los cuales se mide es continua.
Ej: Se tiene una bolsa de bolillas con igual cantidad de bolillas de cada color. Solo hay rojo y amarillo. E sería el espacio muestral del experimento aleatorio que consiste en sacar 3 bolillas de la bolsa, y X sería la función de E al cual cada elemento se le asigna la cantidad de bolillas rojas sacadas. X es una variable aleatoria que toma los valores:
x = 0
x = 1
x = 2
x = 3
Quedaría:
f(0) = P (x=0) = 1/8
f(1) = P (x=1) = 3/8
f(2) = P (x=2) = 3/8
f(3) = P (x=3) = 1/8
TOPOGRAFIA --> Cuadrilatero con un solo angulo recto, poner los datos minimos necesarios para resolver, y luego resolver.
Creo que con darnos la medida de la diagonal que va de D a B, el angulo c y un angulo interno de los triangulos que se forman podemos sacar todo. Perimetro más area.
Perimetro usando reglas del seno o teorema del coseno y area con la formula del area:


martes, 4 de marzo de 2014
DERIVADAS e INTEGRALES: Matematica II Blumenfarb Final.
Faltan 3 dias para rendir. Sin más comentarios empiezo.
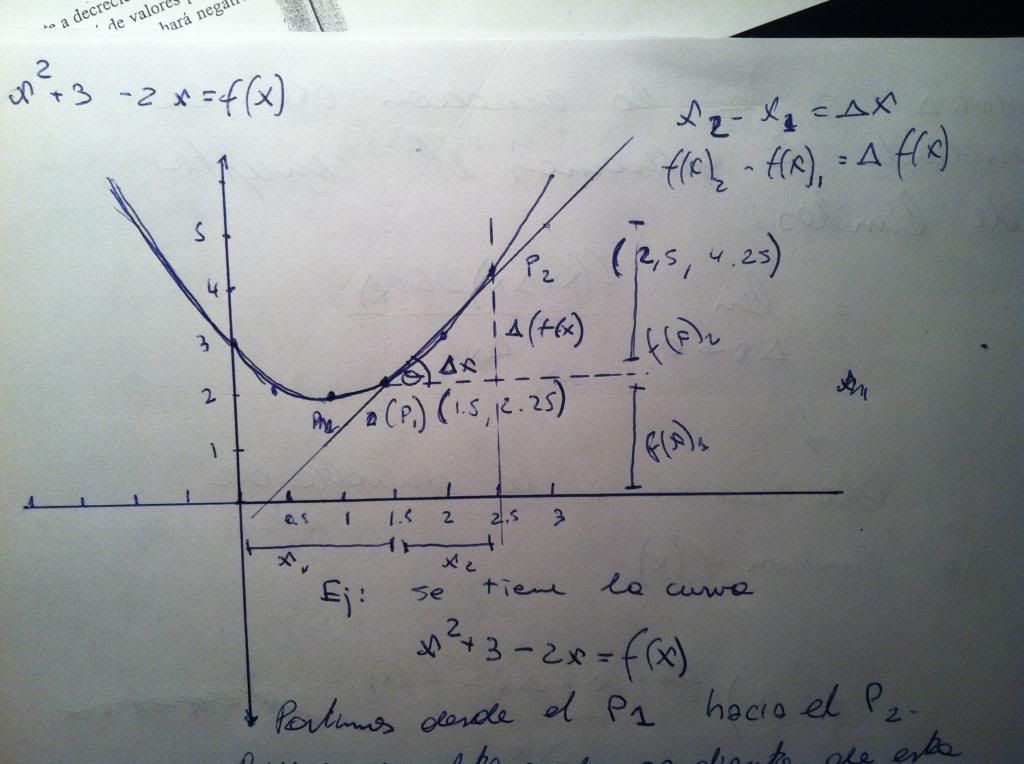
Ej: Se tiene la curva x2 + 3 + 2x = f(x)
![s = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx](http://upload.wikimedia.org/math/e/6/1/e61ceab68a8e7295fadd088701908963.png)

Final Marzo 2013:
-Definir Derivada de una función en un punto. ¿Cuál es su interpretación geometrica? Justificar un ejemplo numérico resuelto mediante la aplicación de esa definición y mediante la regla práctica
La derivada de una función en un punto es la pendiente de la recta tangente a la curva en ese punto.
La interpretación geometrica muestra como se llega a la pendiente de la tangente aplicando el concepto de limite a la ecuación de pendiente de una recta secante.
Ej: Se tiene la curva x2 + 3 + 2x = f(x)
Partimos desde el P1 hacia el P2 y se genera una recta secante. Queremos obtener la pendiente de esta recta secante.
La ecuación de la pendiente es:
Ahora si se aplica el concepto de limite:
__________________
Julio 2013:
Máximos y mínimos: Criterios para calcularos y ejemplo númerico que tenga máximo y mínimo.
Los máximos y mínimos son puntos críticos.
La condición necesaria para que exista un máximo, si existe f ´ (x) y f ´´ (x),
es que f ´ (x) = 0 y f ´´ (x) < 0.
La condición necesaria para que exista un mínimo, si existe f ´ (x) y f ´´ (x),
es que f ´ (x) = 0 y f ´´ (x) > 0.
EJ: f(x) = x3 - 3x2 + 1 = 0
La derivada es f ´ (x) = 3x2 - 6x = 0 (La primera condición ya está para ambos)
Resolviendo la derivada nos da x = 2, x = 0
La segunda derivada es f ´´ (x) = 6x - 6
Para 0 ---- > 6(0) - 6 = -6
-6 < 0 ---- > se trata de un máximo... en el punto de la curva donde x = 0 hay un punto máximo
Para 2 ---- > 6(2) - 6 = 6
6 > 0 ---- > se trata de un mínimo.... en el punto de la curva donde x = 2 hay un punto mínimo
Otro final:
Aplicaciones geometricas de una integral definida.
Las aplicaciones geometricas de una integral definida son Área, volumen y longitud de una curva.
Para calcular el área entre una curva y el eje x se utiliza un integral definido.

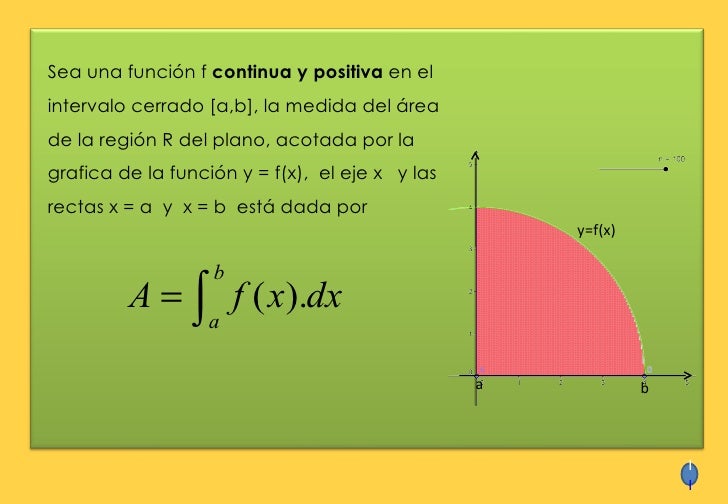
Se utiliza también para medir longitud de una curva con la siguiente formula.
![s = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx](http://upload.wikimedia.org/math/e/6/1/e61ceab68a8e7295fadd088701908963.png)
Finalmente para el volumen tambien se puede utilizar integrales. Sobre todo para cuerpos engendrados por la revolucion de una curva.
Dada la formula f(x) para calcular el volumen de revolución a través del eje ox se utiliza

___________________________________________________
Encontré otra sola pregunta de final diferente a estas, una que tenía que ver con los centros de gravedad y masa ..... para integrales no? pero bueno, como estaba muy poco decido no estudiarlo ya que no llego sino y ademas me da extremada paja porque es un tema denso.
Mañana veo si hago topo.... y ya a repasar examenes enteros para el final.
Suscribirse a:
Comentarios (Atom)