Final Marzo 2013:
-Definir Derivada de una función en un punto. ¿Cuál es su interpretación geometrica? Justificar un ejemplo numérico resuelto mediante la aplicación de esa definición y mediante la regla práctica
La derivada de una función en un punto es la pendiente de la recta tangente a la curva en ese punto.
La interpretación geometrica muestra como se llega a la pendiente de la tangente aplicando el concepto de limite a la ecuación de pendiente de una recta secante.
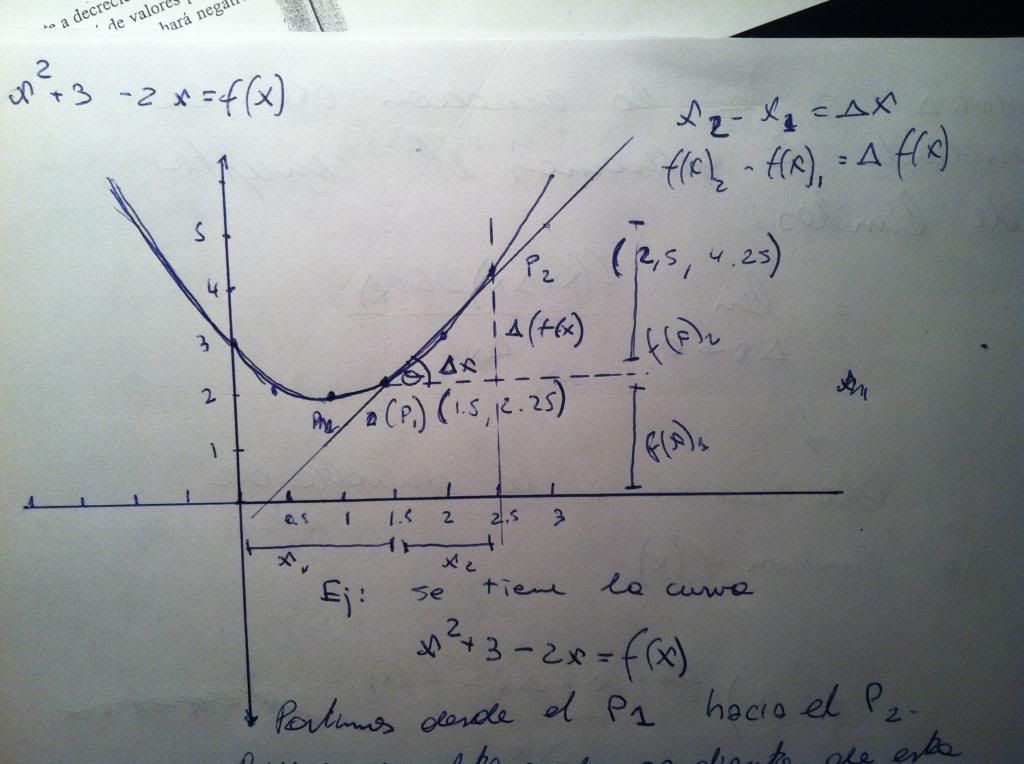
Ej: Se tiene la curva x2 + 3 + 2x = f(x)
Partimos desde el P1 hacia el P2 y se genera una recta secante. Queremos obtener la pendiente de esta recta secante.
La ecuación de la pendiente es:
Ahora si se aplica el concepto de limite:
__________________
Julio 2013:
Máximos y mínimos: Criterios para calcularos y ejemplo númerico que tenga máximo y mínimo.
Los máximos y mínimos son puntos críticos.
La condición necesaria para que exista un máximo, si existe f ´ (x) y f ´´ (x),
es que f ´ (x) = 0 y f ´´ (x) < 0.
La condición necesaria para que exista un mínimo, si existe f ´ (x) y f ´´ (x),
es que f ´ (x) = 0 y f ´´ (x) > 0.
EJ: f(x) = x3 - 3x2 + 1 = 0
La derivada es f ´ (x) = 3x2 - 6x = 0 (La primera condición ya está para ambos)
Resolviendo la derivada nos da x = 2, x = 0
La segunda derivada es f ´´ (x) = 6x - 6
Para 0 ---- > 6(0) - 6 = -6
-6 < 0 ---- > se trata de un máximo... en el punto de la curva donde x = 0 hay un punto máximo
Para 2 ---- > 6(2) - 6 = 6
6 > 0 ---- > se trata de un mínimo.... en el punto de la curva donde x = 2 hay un punto mínimo
Otro final:
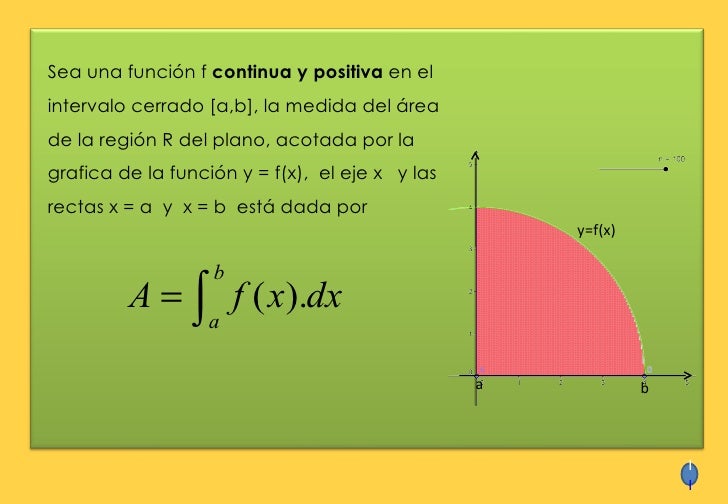
Aplicaciones geometricas de una integral definida.
Las aplicaciones geometricas de una integral definida son Área, volumen y longitud de una curva.
Para calcular el área entre una curva y el eje x se utiliza un integral definido.
Se utiliza también para medir longitud de una curva con la siguiente formula.
![s = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx](http://upload.wikimedia.org/math/e/6/1/e61ceab68a8e7295fadd088701908963.png)
Finalmente para el volumen tambien se puede utilizar integrales. Sobre todo para cuerpos engendrados por la revolucion de una curva.
Dada la formula f(x) para calcular el volumen de revolución a través del eje ox se utiliza

___________________________________________________
Encontré otra sola pregunta de final diferente a estas, una que tenía que ver con los centros de gravedad y masa ..... para integrales no? pero bueno, como estaba muy poco decido no estudiarlo ya que no llego sino y ademas me da extremada paja porque es un tema denso.
Mañana veo si hago topo.... y ya a repasar examenes enteros para el final.


No hay comentarios:
Publicar un comentario